by Matt Ford
[A timeless ode to these remarkable structures. Reprinted here thanks to Matt, who now teaches at UW Tacoma.]
Today [Feb 14], most Americans will be thinking of their loved ones while they frantically try to book dinner reservations. In our mad-cap black-friday-esque dashes to the novelty chocolate and bizarre couple's gifts aisle, many of us will miss an equally-important and no-less contrived holiday: National Ferris Wheel Day.
From the beginning, the engineering community was awed by the wheel. Speaking before a conference of engineers in 1893, William H. Searles summarized what was publicly known about the wheel and its construction.
He went on to give a series of staggering sums: the rim measured 250 feet in diameter; the full weight of the wheel including passengers reached almost 3 million pounds; the spindle alone, the largest forging in the world up to that time, weighed 93 tons. Furthermore, the entire project was supervised by Ferris himself, only 12 years out of school, and the chief engineer, W. F. Gronau, only 5 years out of school.
The Year of the Wheel
The similarity between the Chicago Wheel and its ancestor, the tensioned-spoked bicycle wheel, was not lost on fair attendees:
Prior to 1869, bicycle wheels were constructed in the same fashion (and often by the same craftsmen) as carriage wheels: a heavy, wooden rim was supported by stout wooden spokes which carried the weight of the vehicle through compression. The carriage wheel was heavy and prone to failure. Its diameter was severely limited by the tendency of the spokes to buckle under compression.
The tension-spoked wheel was nothing short of revolutionary: instead of carrying compression, the spokes were given an initial tension in order to prevent them from going slack under the weight of the bike and rider. Eliminating the risk of buckling allowed the use of slender metal wire in place of the thick wooden spokes, permitting larger and lighter wheels. Practically every bicycle wheel ridden today uses this design.
Searles and his audience pondered the similarities between the bicycle wheel and the Ferris Wheel:
Stresses in Wheels
Unlike in the bicycle wheel, the forces on the Ferris Wheel are distributed around its circumference, as Mr. Gifford noted above. The rim acts like two connected arches: the weight of the cars is channeled downwards through the compressive force in the rim, becoming larger and larger until we reach the bottom.
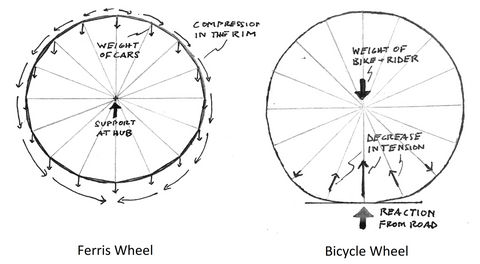
If the weight of the truss is neglected compared with the weight of the cars, the tension in the spokes varies from zero (at the very top) to 4W, where W is the weight of a single car. Interestingly, the stresses in the spokes do not depend on the diameter of the rim or the number of cars. In order to prevent the spokes from going slack, a tension of 2W must be added to each spoke during construction. Ferris and his engineers accomplished this by installing turnbuckles on each spoke and adjusting them manually.
The rim is under compression everywhere. A good approximation, provided there are a sufficient number of spokes, gives the compression in the rim at the top as NW/2π, where N is the number of spokes, and the compression in the rim at the bottom as 3NW/2π. Unlike the spokes, the rim feels the full weight of all the cars at the bottom, and must be designed against buckling. The stresses in the Ferris Wheel are independent of the stiffness of the spokes and rim, so long as the individual components don't fail. This makes the design rather straightforward: once you have selected the number and capacity of the cars, the spokes and rim can be designed using simple formulas. In the bicycle wheel, on the other hand, the stresses in the spokes depend on the number and stiffness of the spokes, the diameter of the wheel, and the stiffness of the rim. The stresses can't be determined from statics alone.
The first quantitative analysis of the bicycle wheel under load was given by Bernard Smith in 1901, 8 years after the fair and 32 years after the introduction of the tension- spoked bicycle wheel. He derived an approximate solution for the deformation of the rim and the stresses in the spokes by assuming that the number of spokes was large enough to be considered infinite: imagine "smearing out" the discrete spokes into a continuous disc of spokes.
He found mathematically what was already known qualitatively at the time, which is that the weight of the hub is supported by the loss of tension in just a few spokes directly underneath the hub. The spokes above the hub, although still under tension, don't change in tension by more than a few percent of the applied load, leading Jobst Brandt and others to say that the hub "stands on the spokes" below it.
Since the load is supported by only a few spokes, the bottom-most spokes ends up carrying about half the total applied load (contrast with the Ferris Wheel, where the bottom spoke carries only 10% of the total weight, for a 36-spoke wheel). Adding more spokes decreases the load borne by any one spoke, but the effect is non-linear: twice the spokes does not equal half the load.
In order to carry you and your bike safely, the bottom-most spoke must not lose tension completely. Therefore, the spokes must be given an initial tension at least equal to half the load on the wheel. In practice, spokes on modern wheels are usually tensioned to about 100 kgf, more than enough, generally, to support large loads from potholes or side forces. The rim must in turn bear a compressive force equal to NT/2π, where T is the initial tension in each spoke. Most of the time, our bicycle wheels take on this huge responsibility without complaint, though not always, as seen below:
Giant Bicycle Wheels
Modern Ferris wheels (more generally "Observation Wheels") tend to look more like bicycle wheels, with continuous, thickened rims, and a web of slender cables for spokes. The original Ferris Wheel depended on diagonal braces to brace the truss against the notorious Chicago gales. The hub of the Chicago Wheel was relatively wide (45.5 ft) compared with its diameter (250 ft), an aspect ratio of 18%. These modern wheels are noticeably more slender (though I was unable to find measurements of the hub widths). Under these conditions, the spokes must be designed with enough pretension so that they don't go slack when supporting wind loads.
At larger diameters and spoke tensions, buckling of the rim becomes a concern. A bicycle wheel can "taco" under excessive tension, and large observations wheels are no different. A careful optimization routine was carried out for each to determine the necessary tension to support the rim without going slack, then the rim stiffness needed to prevent buckling, then optimizing the rim for weight and iterating the entire process again.
If you're lucky enough to live near a Ferris wheel, take a friend or lover on a leisurely spin, and enjoy Valentine's Day at the pace it was meant to be enjoyed.
To learn more about the mechanics of bicycle wheels:
Peruse this website, or read my Ph.D. thesis.
References
Ferris Wheel, Wikipedia.
London Eye, Wikipedia.
Singapore Flyer, Wikipedia.
High Roller (Ferris wheel), Wikipedia.
David Lazarus, Column: Valentine's Day, so lucrative for businesses, has a naughty history, Chicago Tribune, February 14th, 2017.
George Washington Gale Ferris, the Ferris Wheel, Wikipedia.
Johnson, Bryan, and Turneaure, The Theory and Practice of Modern Framed Structures, London (1895).
W.H. Searles, The Ferris Wheel, Journal of the Association of Engineering Societies
Discussion: Stresses in the Ferris Wheel, Engineering News and American Railway Journal, 31, 349–350 (1894)
B.A. Smith, The Bicycle Wheel. Report of the Meeting of the Australasian Association for the Advancement of Science, 8:197–203, (1901).
Jobst Brandt, The Bicycle Wheel (1993).
Comments will be approved before showing up.